-
Viewpoint on 'IONS'
Viewpoint on 'Scientific Literacy'
- Proudly sponsored by
-

-
Quantum Devices to Thrive on Disorder
It is usually assumed that a greater effort to perfect control and order in a device is rewarded by better results. However, imperfection and disorder could be a state of contentment when it comes to photon trapping.
-
Happy Birthday Laser!

This year the world celebrates the 50th birthday of the laser through an initiative jointly organized by various optics and photonics organizations: the LaserFest. Happy birthday laser!
-
A New Twist to Optical Detectors

A new arrival in the family of optical detectors gives a new twist to the detection of the orbital angular momentum of light. This could make classical and quantum optical communications even easier.
Volume 4 Story 4 - 2/3/2009
Pouring Oil on Troubled
What happens when light enters a medium? Does it gain or lose momentum? More than 100 years after its initial formulation, this dilemma is now being revitalized by new experiments.
Few physical problems have withstood the attack of generations of great scientists as has the Abraham-Minkowski dilemma: in 1908, Minkowski proposed that the momentum of a photon should increase when entering a medium; then, one year later in 1909, Abraham argued that it must decrease. Since then, scientists’ opinion on this matter has been swinging to and from the two positions. A new experiment now being performed by Weilong She and colleagues of Zhongshan University in Guangzhou (China) is pouring new oil on this troubling quandary.
The Abraham-Minkowski dilemma has arisen due to the of the lack of definitive experimental evidence favoring one theory or the other and the fact that both approaches can be supported by reasonable arguments. Let us have a look at the most intuitive arguments in favor of each theory.
In the case of Minkowski’s approach, we are led to explore an argument from quantum physics — even though Minkowski, who died in 1909, did not possess any knowledge base of quantum physics. The momentum p carried by a photon is inversely proportional to its wavelength λ, that is p = h/λ, with h being the Planck constant. When a photon enters a dielectric medium with refractive index n, its wavelength becomes shorter, that is λ/n. Ergo, Minkowski’s (simplified) syllogism states that if the momentum is inversely proportional to the wavelength and the wavelength decreases by a factor of n, then the momentum must increase by a factor of n.
Abraham, on the other hand, was very fond of the intuitive concepts of classical physics; for instance, he hoped that some experiments would demonstrate the existence of the ether, proving Einstein’s relativity theory wrong, until the end of his days in 1922. His approach is consequently rooted in the classical definition of momentum. In classical physics, the momentum of an object is proportional to its velocity. Therefore, since the speed of a photon in a dielectric medium decreases by a factor of n, its momentum must also decrease by a factor of n.
It is puzzling how logical and sound both arguments are and yet, at the same time, they can even be made more rigorous! This leads to deep theoretical justifications for both Abraham and Minkowski. However, it is not possible for both scientists to be correct at the same time. Therefore, it is important to remember that even though theoretical arguments can be convincing to a high degree, the garland for a physicist is to find which theory can be verified experimentally.
Certainly physicists have tried hard to find experimental evidence either in favor of Minkowski or in favor of Abraham. Nevertheless, they have not yet been able to definitively resolve the dilemma. Why? Iver Brevik from the Norwegian University of Science and Technology (NTNU, Norway) explains, "the major obstacle for the experimental resolution of the energy-momentum problem […] is that most experiments in optics are testing the electromagnetic surface force only." These forces are the same for both the Abraham and the Minkowski approach, and therefore lead to the same observable effects.
In a nutshell, we have no definitive experimental evidences favoring either Minkowski or Abraham — and the ones we do have, seem to slightly favor Minkowski’s interpretation.
For example, let us consider the famous Ashkin-Dziedzic pressure experiment dating back to 1973. They showed that a narrow light beam impinging on a free liquid surface acts on the surface by an outward pull. This results in the water surface bulging outward [1,2]. This appeared to be consistent with the sign of the value of the Minkowski momentum: the bulge would be the result of the decreased light momentum in air. However, it was later shown that the effect is governed by a radial force — the water tends to collect in the high-intensity region of the laser beam, therefore the bulge — and that it provides no information on the longitudinal force associated with the linear momentum of light. Conclusion: nothing definitive came out of this experiment!
Similar behaviors were also found in successive experiments. The Zhang-Chang experiment (1988) observed the oscillations of a small water droplet illuminated by a laser pulse [3]. In the optical stretcher experiment of Guck and coworkers [4], a biological cell was positioned between two counter-propagating laser beams and stretched, with the amount of stretching being dependent on the elasticity properties of the cell.
"There are a few experiments in which electromagnetic momentum is measured directly," adds Brevik. "The Jones-Richards experiment [4] and the subsequent Jones-Leslie experiment [5] tested the momentum of an optical wave by measuring the radiation force on a metallic wall of rhodium-plated silver mirror immersed in a dielectric liquid. Another experiment of essentially the same kind is the photon recoil experiment of Campbell et al. [6]. Both these experiments showed that it is the Minkowski tensor that is appropriate for describing the photon in a medium."
The new experiment performed by Weilong She and colleagues seems to support Abraham’s interpretation. They shined laser light through the cleaved core of an optical fiber only half a micron wide and a few millimeters long. "We thought that, as the silica filament is a solid and so light," explains Weilong She, "its free end would be pushed to move backward if Abraham´s momentum theory applies [the light momentum in the medium is smaller than in free space] or be pulled forward if Minkowski´s momentum theory applies [the light momentum in the medium is larger than in free space], when light emerges from the free end." And indeed the researchers observe the recoil of the optical fiber whenever a laser pulse leaves the fiber that should point toward Abraham’s interpretation.
What is the novelty of Weilong She’s experiment? Weilong She explains that their "silica filament is a solid, different from the air-water interface, which is influenced evidently by the lateral gradient force of a Gaussian beam." From this point of view, Weilong She’s experiments seem to deliver a more robust experimental evidence than, for example, the water-bulge experiment. However, we must take into account Brevik’s opinion: "the paper of She et al. falls, in my opinion, into the same category as the experiments above. The experiment is quite interesting, as it shows the action of pressure forces on thin fibers. But I cannot understand that it measures electromagnetic momentum." In addition, Miles Padgett from the Department of Physics and Astronomy of the University of Glasgow (UK), shares a similar opinion: "it is an extremely interesting experiment I wish I had done myself. However, I do not think of it as a claim that Minkowski is wrong [and therefore that Abraham is right]."
One thing is clear; the last word on the Abraham-Minkowski dilemma has not yet been said. In Miles Padgett’s words, "this is an interesting debate, which has been around for over one hundred years. I am sure the dilemma will last a few years more."
[1] A. Ashkin and J. M. Dziedzic, Radiation Pressure on a Free Liquid Surface, Phys. Rev. Lett. 30, 139-142 (1973).
[2] I. Brevik, Experiments in phenomenological electrodynamics and the electromagnetic energy-momentum tensor, Phys. Rep. 52, 133 (1979).
[3] J. Z. Zhang and R. K. Chang, Shape distortion of a single water droplet by laser-induced electrostriction, Opt. Lett. 13, 916 (1988).
[4] J. Guck et al., The Optical Stretcher: A Novel Laser Tool to Micromanipulate Cells, Biophys. J. 81, 767 (2001).
[5] R. V. Jones and J. C. S. Richards, The Pressure of Radiation in a Refracting Medium, Proc. Roy. Soc. London Ser. A 221, 480 (1954).
[6] R. V. Jones and B. Leslie, The Measurement of Optical Radiation Pressure in Dispersive Media, Proc. Roy. Soc. London Ser. A 360, 347 (1978).

Pouring Oil on Troubled
Light-Momentum
What happens when light enters a medium? Does it gain or lose momentum? More than 100 years after its initial formulation, this dilemma is now being revitalized by new experiments.
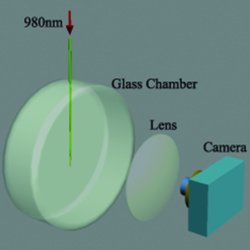
Experimental setup. A silica filament hanging in vacuum is observed while the light bends it. Picture courtesy of Weilong She.
The Abraham-Minkowski dilemma has arisen due to the of the lack of definitive experimental evidence favoring one theory or the other and the fact that both approaches can be supported by reasonable arguments. Let us have a look at the most intuitive arguments in favor of each theory.
In the case of Minkowski’s approach, we are led to explore an argument from quantum physics — even though Minkowski, who died in 1909, did not possess any knowledge base of quantum physics. The momentum p carried by a photon is inversely proportional to its wavelength λ, that is p = h/λ, with h being the Planck constant. When a photon enters a dielectric medium with refractive index n, its wavelength becomes shorter, that is λ/n. Ergo, Minkowski’s (simplified) syllogism states that if the momentum is inversely proportional to the wavelength and the wavelength decreases by a factor of n, then the momentum must increase by a factor of n.

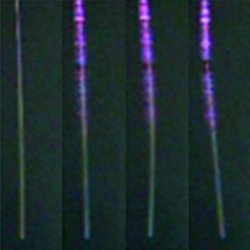
Is the light gaining momentum? The recoil of the fiber (from left to right) would suggest that the light is gaining momentum while exiting the fiber. Picture courtesy of Weilong She.
It is puzzling how logical and sound both arguments are and yet, at the same time, they can even be made more rigorous! This leads to deep theoretical justifications for both Abraham and Minkowski. However, it is not possible for both scientists to be correct at the same time. Therefore, it is important to remember that even though theoretical arguments can be convincing to a high degree, the garland for a physicist is to find which theory can be verified experimentally.
Certainly physicists have tried hard to find experimental evidence either in favor of Minkowski or in favor of Abraham. Nevertheless, they have not yet been able to definitively resolve the dilemma. Why? Iver Brevik from the Norwegian University of Science and Technology (NTNU, Norway) explains, "the major obstacle for the experimental resolution of the energy-momentum problem […] is that most experiments in optics are testing the electromagnetic surface force only." These forces are the same for both the Abraham and the Minkowski approach, and therefore lead to the same observable effects.
In a nutshell, we have no definitive experimental evidences favoring either Minkowski or Abraham — and the ones we do have, seem to slightly favor Minkowski’s interpretation.
For example, let us consider the famous Ashkin-Dziedzic pressure experiment dating back to 1973. They showed that a narrow light beam impinging on a free liquid surface acts on the surface by an outward pull. This results in the water surface bulging outward [1,2]. This appeared to be consistent with the sign of the value of the Minkowski momentum: the bulge would be the result of the decreased light momentum in air. However, it was later shown that the effect is governed by a radial force — the water tends to collect in the high-intensity region of the laser beam, therefore the bulge — and that it provides no information on the longitudinal force associated with the linear momentum of light. Conclusion: nothing definitive came out of this experiment!
Similar behaviors were also found in successive experiments. The Zhang-Chang experiment (1988) observed the oscillations of a small water droplet illuminated by a laser pulse [3]. In the optical stretcher experiment of Guck and coworkers [4], a biological cell was positioned between two counter-propagating laser beams and stretched, with the amount of stretching being dependent on the elasticity properties of the cell.
"There are a few experiments in which electromagnetic momentum is measured directly," adds Brevik. "The Jones-Richards experiment [4] and the subsequent Jones-Leslie experiment [5] tested the momentum of an optical wave by measuring the radiation force on a metallic wall of rhodium-plated silver mirror immersed in a dielectric liquid. Another experiment of essentially the same kind is the photon recoil experiment of Campbell et al. [6]. Both these experiments showed that it is the Minkowski tensor that is appropriate for describing the photon in a medium."
The new experiment performed by Weilong She and colleagues seems to support Abraham’s interpretation. They shined laser light through the cleaved core of an optical fiber only half a micron wide and a few millimeters long. "We thought that, as the silica filament is a solid and so light," explains Weilong She, "its free end would be pushed to move backward if Abraham´s momentum theory applies [the light momentum in the medium is smaller than in free space] or be pulled forward if Minkowski´s momentum theory applies [the light momentum in the medium is larger than in free space], when light emerges from the free end." And indeed the researchers observe the recoil of the optical fiber whenever a laser pulse leaves the fiber that should point toward Abraham’s interpretation.
What is the novelty of Weilong She’s experiment? Weilong She explains that their "silica filament is a solid, different from the air-water interface, which is influenced evidently by the lateral gradient force of a Gaussian beam." From this point of view, Weilong She’s experiments seem to deliver a more robust experimental evidence than, for example, the water-bulge experiment. However, we must take into account Brevik’s opinion: "the paper of She et al. falls, in my opinion, into the same category as the experiments above. The experiment is quite interesting, as it shows the action of pressure forces on thin fibers. But I cannot understand that it measures electromagnetic momentum." In addition, Miles Padgett from the Department of Physics and Astronomy of the University of Glasgow (UK), shares a similar opinion: "it is an extremely interesting experiment I wish I had done myself. However, I do not think of it as a claim that Minkowski is wrong [and therefore that Abraham is right]."
One thing is clear; the last word on the Abraham-Minkowski dilemma has not yet been said. In Miles Padgett’s words, "this is an interesting debate, which has been around for over one hundred years. I am sure the dilemma will last a few years more."
[1] A. Ashkin and J. M. Dziedzic, Radiation Pressure on a Free Liquid Surface, Phys. Rev. Lett. 30, 139-142 (1973).
[2] I. Brevik, Experiments in phenomenological electrodynamics and the electromagnetic energy-momentum tensor, Phys. Rep. 52, 133 (1979).
[3] J. Z. Zhang and R. K. Chang, Shape distortion of a single water droplet by laser-induced electrostriction, Opt. Lett. 13, 916 (1988).
[4] J. Guck et al., The Optical Stretcher: A Novel Laser Tool to Micromanipulate Cells, Biophys. J. 81, 767 (2001).
[5] R. V. Jones and J. C. S. Richards, The Pressure of Radiation in a Refracting Medium, Proc. Roy. Soc. London Ser. A 221, 480 (1954).
[6] R. V. Jones and B. Leslie, The Measurement of Optical Radiation Pressure in Dispersive Media, Proc. Roy. Soc. London Ser. A 360, 347 (1978).
Giovanni Volpe
2009 © Optics & Photonics Focus
GV is currently working as a postdoctoral researcher at the Max Planck Institute in Stuttgart (Germany).

Weilong She, Jianhui Yu, and Raohui Feng, Observation of a Push Force on the End Face of a Nanometer Silica Filament Exerted by Outgoing Light, Physical Review Letters (2008) 101, 243601 (link).