-
Viewpoint on 'IONS'
Viewpoint on 'Scientific Literacy'
- Proudly sponsored by
-

-
Pouring Oil on Troubled Light-Momentum

What happens when light enters a medium? Does it gain or lose momentum? More than 100 years after its initial formulation, this dilemma is now being revitalized by new experiments.
-
Another Brick in the Nanowall

Scientists, just as nano-architects would, are exploring different ways to design nanostructures with fine control over shape and position. A brand-new approach now allows one to build 2D nanowalls up by laying them down brick by brick.
-
Your Eyes Can Write

Our eyes perceive our surroundings, convey emotion and, some may say, that they can even speak, loud and clear. Now, with the help of an optical illusion, our eyes can also write.
THE VIEWPOINT by Yaroslav Kartashov
Optical Lattice Solitons:
Guiding and Routing Light at Will
Optical solitons are localized nonlinear excitations, which exist due to the mutual balance of diffraction and nonlinearity (in the case of spatial solitons) or dispersion and nonlinearity (in the case of temporal solitons). Moreover, they can propagate undistorted over indefinitely long distances. Being nonlinear objects, solitons may interact with each other, sometimes elastically, as if they were mechanical particles, or inelastically, when several solitons may merge together or give birth to new solitons after interaction. In the case of spatial solitons, the transverse modulation of the refractive index of the nonlinear material drastically affects their properties and affords new tools for the control of soliton propagation dynamics. Here, we review some possibilities for soliton control offered by periodic lattices and lattices produced by nondiffracting light beams.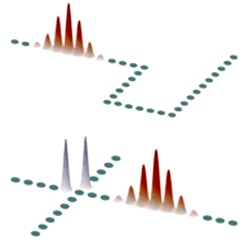
Possible applications of discrete solitons. Upper row: A nonlinear array network involving consecutive bends. The waveguide cross-sections are shown in green. A discrete soliton, shown in red, is set in motion in this system by appropriately tilting the beam. Computer simulations indicate that discrete soliton can successfully negotiate a sequence of bends. Lower row: An X-switching junction that uses two different discrete soliton families, signal (red) and blockers (blue). Unlike signal, which are highly mobile, blockers tend to retain their position after a collision event. After incoherent collision, the signal soliton is routed toward the lower branch, because of the presence of the two blockers at the entries of the respective pathways.
Nonlinear wave excitations evolving undistorted are usually termed solitons. Solitons have been the subject of intense theoretical and experimental investigation in many different fields. The history of solitons in fact starts in 1834 when J. S. Russell observed that a heap of water in a canal propagated undistorted over several kilometers. The term "soliton" was adopted in 1965 to reflect the particle-like nature of solitons that remained undistorted even after mutual collision, although now this term is used in a broader context, to denote any localized nonlinear excitation that remains unchanged upon evolution.
In the context of nonlinear optics, solitons are usually classified as temporal or spatial, depending on whether the confinement occurs in time or in space. Temporal solitons represent optical pulses that keep their temporal shapes, while spatial solitons represent self-guided beams that keep the transverse intensity distributions in the plane orthogonal to the propagation direction. Both types of solitons appear due to nonlinear change of the refractive index of the material induced by the light intensity.
In nonlinear optics a phenomenon known as Kerr effect generates the refractive index change: the intensity dependence of refractive index leads to spatial self-focusing (or self-defocusing) and temporal self-phase modulation. It is this nonlinear effect that is responsible for the formation of optical solitons. A spatial soliton is formed when the self-focusing of an optical beam exactly balances its spreading in the transverse plane due to diffraction. On the other hand, self-phase modulation balances natural dispersion-induced broadening of an optical pulse and leads to the formation of temporal soliton. The earliest example of a spatial soliton corresponds to the 1964 discovery of the nonlinear phenomenon of self-trapping of continuous-wave optical beams in a bulk uniform nonlinear medium, while an example of bright temporal soliton was found in 1973, when it was discovered that optical pulses can propagate inside an optical fiber without changing their shape if they experience anomalous dispersion. Since then, fiber solitons have found practical applications in designing long-haul fiber-optic communication systems. Subsequently, a number of new types of optical solitons were discovered, including spatiotemporal solitons confined in both space and time, Bragg solitons, vortex solitons, solitons existing due to various parametric nonlinear processes (such as quadratic solitons), lattice solitons, etc (for a general overview see [5]).
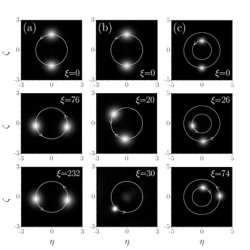
Solitons on a Bessel lattice. (a) The interaction of out-of-phase solitons in the first ring of zero-order Bessel lattice. One of the solitons is set into motion at the entrance of the medium by imposing the phase twist on it. (b) The same as in column (a) but for in-phase solitons. (c) The interaction of out-of-phase solitons located in the first and second lattice rings. The soliton located in the first ring is set into motion by imposing the phase twist. Soliton angular rotation directions are depicted by arrows, while white rings denote rings of Bessel lattice where solitons are located. The distances at which intensity distributions are shown are indicated on each plot.
Interestingly, until recently the research in this area was commonly divided into two distinct, separated categories: solitons in inhomogeneous systems that can be described by continuous mathematical models, and systems that are effectively described by discrete equations. In fact, however, there is a whole world in between systems modeled by totally continuous and totally discrete evolution equations. This world has been made accessible to experimental exploration in its full scope only recently, with the advent of totally tunable optically-induced lattices produced by different types of nondiffracting beams in optics [7] and Bose-Einstein condensates [8]. Tuning the strength of the lattices causes the behavior of an inhomogeneous system to vary between a predominantly continuous to a predominantly discrete system. The corresponding power concept termed tunable discreteness has direct and important applications, e.g., for all-optical routing and shaping of light in optics, or for the generation and manipulation of quantum correlated matter waves in Bose-Einstein condensates. In addition to such applications, from a broad perspective, the ability to tune the strength of the genuinely discrete features of the inhomogeneous nonlinear systems affords important applications in other areas of nonlinear science where the concept can be implemented. Optical lattices provide a unique laboratory to undertake such exploration.
As it was mentioned above, the propagation of light in media whose properties vary periodically along the transverse direction exhibits a wealth of opportunities for all-optical light control. For example, in arrays of evanescently coupled waveguides, optical radiation can be transferred across the array because of the coupling between neighboring lattice sites, which manifests itself in the phenomenon of discrete diffraction, that replaces the usual diffraction in uniform medium.
Importantly, by changing the angle of incidence of laser beams in linear lattices (or so-called Bloch momentum) one can tune the sign and absolute value of the diffraction coefficient, thus suppressing or even reversing the diffraction process, which is impossible in uniform medium, where the diffraction coefficient is fixed by the material and the radiation wavelength. In nonlinear waveguide arrays, optical radiation can trap itself. A key parameter here is the competition between such characteristic scales of the problem as the beam width and the waveguide spacing in the array. In the case of appropriate balance, when nonlinear self-action exactly compensates discrete diffraction, an optical soliton that is confined only on several waveguides can be formed. Depending on the nature of the underlying nonlinear process, different families of discrete solitons are possible. Arrays made from materials with intensity-dependent Kerr, quadratic, or photorefractive nonlinearities have been shown to support one- and two-dimensional discrete solitons [9,10]. Because of their unique properties such discrete solitons are extremely suitable candidates for the design of soliton-based, all-optical photonic circuits and devices. Discrete solitons can survive upon propagation through lattice bends; they can be trapped in different lattice channels depending on the incidence angle; discrete soliton mobility decreases with the increase of spatial localization so that interactions between several solitons can be used for all-optical routing, blocking, and construction of logic gates (Fig. 1).
In the case of optical lattice induction, another scenario is encountered when optical radiation enters nonlinear media with the imprinted harmonic transverse modulation of the refractive index. Such nonlinear harmonic lattices support stable lattice solitons, whose properties may depart considerably from that of usual discrete solitons. Two-dimensional lattice solitons were recently observed in optically induced lattices in photorefractive crystals that allow almost linear propagation of light in one polarization (lattice-creating component) and highly nonlinear propagation in the other (soliton-creating component). Notice that harmonic lattices in photorefractive crystals can easily be created by interfering plane wave pairs, whose interference pattern (hence, induced refractive index landscape) remains unchanged in propagation direction. Despite the fact that neighboring guides in harmonic lattices are always strongly coupled, by changing the depth of refractive index modulation one can indeed tune the system properties from quasi-continuous (at low modulation depth) to completely discrete (at considerable modulation depth). Therefore, an intermediate regime constituted by continuous nonlinear media with imprinted modulation of refractive index offers a number of new opportunities. From the experimental viewpoint, optically induced lattices might operate on both weakly and strongly coupled regimes, thus offering the above-mentioned tuneability. Besides simplest soliton states, nonlinear lattices may support a variety of higher-order solitons including multipoles, vortices, and soliton trains, that are highly unstable or do not exist in the corresponding uniform medium. Such solitons form when several of the lowest order lattice solitons are packed together with appropriately engineered phases. This immediately suggests the important possibility to construct and to manipulate multi-peaked soliton packets beyond single soliton bits, a feature that may open a new door in all optical-switching schemes.
Importantly, besides the simplest optical lattices featuring interference patterns of several plane waves (plane wave is a simplest nondiffracting wave in uniform medium) the lattices with different types of symmetry can also be created, and may offer reach opportunities for soliton existence, managing, and control [10]. Propagation of all linear beams in uniform media is described by the three-dimensional Helmholtz equation that admits separation into the transverse and longitudinal parts only in Cartesian, circular cylindrical, elliptic cylindrical, and parabolic cylindrical coordinates. Each of these coordinate systems then give rise to a certain type of nondiffracting beam associated with a fundamental solution of Helmholtz equation in this coordinates. Using such beams for optical induction opens broad prospects for the creation of refractive index landscapes with novel types of symmetry. The lattices produced with nondiffracting Bessel beams are particularly interesting. The cylindrical geometry of the lattice, with several concentric rings, affords unique soliton properties and dynamics. In particular, besides the lowest-order solitons trapped in the center of the lattice, one can find soliton families trapped at different lattice rings that can be set into controlled rotation inside each ring, thus featuring novel types of in-ring and inter-ring soliton interactions as shown in Fig. 2. The possibility to set solitons into rotary and almost radiationless motion in radially symmetric lattices opens broad prospects for all-optical routing. Stationary and dynamical Bessel lattices produced by higher-order nondiffracting Bessel beams can support stable necklace-like soliton complexes and might be utilized for specific azimuthal soliton switching; arrays of Bessel beams can be implemented to build reconfigurable soliton networks and wires. Lattices induced by parabolic nondiffracting beams support stable higher-order solitons with unusual symmetries, etc. All this indicates that optical lattices may support a rich variety of new soliton families, could lead to new dynamical phenomena, and perhaps offer novel conceptual opportunities for all-optical shaping, switching and routing of optical signals encoded in soliton formats.
The field of optical dynamics in nonlinear optical lattices is at an exciting stage of development. Even though some of the basic concepts have been around for a while, much remains to be understood and discovered. The recent progress in technique of fabrication and induction of nonlinear lattices allow one to access the potential of these structures for use in tomorrow’s optical communication systems and switching networks.
[1] E. Infeld and R. Rowlands, Nonlinear waves, solitons and chaos (Cambridge University Press, Cambridge, 1990).
[2] G. B. Whitham, Linear and nonlinear waves (Wiley, New York,1999).
[3] J. V. Moloney and A. C. Newell, Nonlinear optics (Westview Press, Oxford, 2004).
[4] N. N. Akhmediev and A. Ankiewicz, Solitons – nonlinear pulses and beams (Springer, Berlin, 1997).
[5] Y. S. Kivshar and G. Agrawal, Optical solitons: from fibers to photonic crystals (Academic Press, London, 2003).
[6] G. I. Stegeman and M. Segev, Optical spatial solitons and their interactions: universality and diversity, Science 286, 1518-1523 (1999).
[7] J. W. Fleischer, M. Segev, N. K. Efremidis, and D. N. Christodoulides, Observation of two-dimensional discrete solitons in optically induced nonlinear photonic lattices, Nature 422, 147-150 (2003).
[8] O. Morsch and M. Oberthaler, Dynamics of Bose-Einstein condensates in optical lattices, Rev. Mod. Phys. 78, 179-215 (2006).
[9] F. Lederer, G. I. Stegeman, D. N. Christodoulides, G. Assanto, M. Segev, and Y. Silberberg, Discrete optical solitons, Phys. Rep. 463, 1-126 (2008).
[10] Y. V. Kartashov, V. A. Vysloukh, and L. Torner, Soliton shape and mobility control in optical lattices, Progress in Optics 52, 63-148 (2009).
Yaroslav Kartashov
2009 © Optics & Photonics Focus
Yaroslav Kartashov is Ramón y Cajal research fellow at ICFO - The Institute of Photonic Sciences in Barcelona (Spain). He is one of the most prolific authors in the soliton field with over 100 peer-reviewed articles.
