-
Viewpoint on 'IONS'
Viewpoint on 'Scientific Literacy'
- Proudly sponsored by
-

-
Hack Me If You Can

Quantum cryptography promises inherently secure communications… in theory! But what actually happens in practice? Recent studies show how weaknesses in a real system can be exploited to perform an “undetectable” quantum hack.
-
Thermal Images at the Nanoscale
How would you measure the temperature of a nanoscopic object? How would you build a nano-thermometer? A new technique offers a solution.
-
Magical Metamaterials

Magic lies in the beauty of a powerful illusion. This is what the latest achievements in optics seem to suggest; metamaterials are now able to optically turn one object into another.
Truly Random Results:
You Can Bet on It!
True randomness can hardly ever be proved. However, latest experiments on quantum systems deliver truly random results — guaranteed!
A random guess. Attempting to guess the random draw of the lottery is a matter of pure luck, even though, in principle, these draws can be described by deterministic laws of physics.
Randomness is an important ingredient in many fields of science, technology and, of course, gambling. However, most processes that we call random are typically no more than something that is unpredictable to us, but not truly random. For example, if you are playing the lottery, you rely on the draw to be random — and random, in this case, simply means that all participants have the same chance of winning the jackpot. If you were able to know the exact positions of every lottery ball, the exact movement of the container, all the air currents and everything else influencing the draw, you could, in fact, predict the winning numbers! The reason why we call the outcome of the draw random is simply the fact that there are too many parameters to keep track of, which prevents us from being able to predict it.
There are, however, intrinsically random processes in nature: the decay of atoms or the result when measuring certain quantum states, for example. In fact, this bold claim of intrinsic randomness was so revolutionary in the early days of quantum mechanics, that Albert Einstein famously refuted it. In short, quantum mechanics predicted a new type of instantaneous correlations between distant particles called entanglement. Einstein and his co-workers were convinced that such correlations could only be a simplified (effective) description of an underlying effect which was intrinsically deterministic. Since quantum physics, however, described a probabilistic (random) process in which the physical system did not always define all of its properties deterministically, Einstein and many others were convinced that something had to be missing in quantum theory. Together with other scientists of his day, he therefore developed a Gedankenexperiment (a thought experiment) involving measurements on particles that were distant but also correlated, which raised doubts on the completeness of quantum theory [1]. From the point of view of randomness, one implication of their claim was that true randomness was only an illusion originating from a lack of information or an excess of complexity. According to Einstein's picture of the world, things had to be predictable.
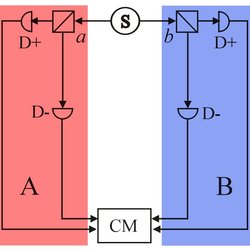
Entanglement and randomness. In Bell-type experiments, the correlations of two distant particles are indicating if these distant objects are entangled or not. Two parties A and B take independent measurement a and b of presumably entangled objects originating from a source S. Each measurement can have outcome D+ or D-. A Coincidence measurement (CM) allows to determine if the experimental results can be explained by classical (hidden variable) theories. Thus if the particles are entangled, no classical correlations (and thus no cheating) can explain the outcome of the measurements and it is possible to generate truly random numbers.
Just like Einstein's objection, however, Bell's proposal was far beyond the technical possibilities of his time. Not surprisingly, it took almost twenty years until the first conclusive experiments could finally be performed. "The Bell experiments of 1982 [3]," Acín explains, "indicated that non-local quantum correlations did exist in nature and showed that Einstein's claim of hidden variables was wrong. At the same time, this meant that quantum physics had to be taken very seriously and that intrinsic randomness was a fact."
Acín and coworkers now produced truly random numbers by inverting the experiments that disproved the existence of hidden variables. "We based ourselves on the fact that the violation of Bell-type inequalities implies that there was intrinsic randomness in the system," Acín explains. "Once we know that it is impossible to create all of our resulting numbers by non-random processes, we can compute which proportion of our experiment was intrinsically random." In essence, the researchers measure to what extent they have created non-local correlations in their experiment. For a fully entangled system, all numbers would be random. For a set of numbers originating from a noisy entangled system, the entire draw would not be certifiably random. Therefore, the researchers calculated bounds describing how many truly random numbers could be extracted in this case. Hereby, their approach allows us to deduce the amount of randomness extractable from an entangled setup.
"The generation of truly random numbers is a great conceptual and technological achievement!" Valerio Scarani [4] from the Center for Quantum Technologies at the National University of Singapore says. "The big step achieved in this research," he points out, "is that we are now able to quantify the intrinsic randomness based on the violation of the Bell-type inequalities." Scarani thinks that this new possibility will be highly relevant whenever people want to be sure that they are really dealing with true randomness. As an example, it is now possible to check if a quantum cryptography system is really using safe random numbers or if somebody might be cheating.
"Quantum information brought about a new way of reasoning," Scarani points out, "which is really starting to have a great impact on the way we approach open problems." Random numbers, quantum algorithms, or even fundamental concepts of physics [5] are very active fields of research today. "The number of links from quantum information to cryptography, computing, fundamental physics, and even applied science, according to both scientists," Acín concludes, "is truly inspiring. And if the past achievements give any indication of what lies ahead, we can really look forward to an extremely interesting future!"
[1] A. Einstein, B. Podolsky & N. Rosen, Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 47, 777–780 (1935).
[2] J.S. Bell, On the Einstein Podolsky Rosen paradox, Physics 1, 195-200 (1964).
[3] A. Aspect, J. Dalibard & G. Roger, Experimental test of Bell's inequalities using time-varying analyzers, Phys. Rev. Lett. 49, 1804-1807 (1982).
[4] V. Scarani, Quantum Physics: A First Encounter: Interference, Entanglement, and Reality, Oxford University Press, New York (2006).
[5] M. Pawlowski et al., Information causality as a physical principle, Nature 461, 1101-1104 (2009).
Armand Niederberger
2010 © Optics & Photonics Focus
AN is currently working on his PhD on disordered ultracold quantum systems at ICFO - The Institute of Photonic Sciences in Barcelona (Spain).

S. Pironio, A. Acín, S. Massar, A. Boyer de la Giroday, D. N. Matsukevich, P. Maunz, S. Olmschenk, D. Hayes, L. Luo, T. A. Manning & C. Monroe, Random numbers certified by Bell’s theorem, Nature (2010) 464, 1021-1024 (link).